El pensamiento crítico como estrategia de mejora en el área de matemáticas
Critical Thinking as a strategy for improvement in the area of Mathematics
Francisco de Jesús Soto Huizar
Escuela Secundaria Técnica #28 (San Francisco del Mezquital, Durango, México)
Resumen
Dada la necesidad de mejorar los niveles de desempeño en las áreas de matemáticas y español, la Escuela Secundaria Técnica # 28 toma acciones para diseñar una estrategia que permita mejorar los resultados al inicio del ciclo escolar 2021-2022 y los cursos posteriores; esos resultados tenían a la escuela identificada por su bajo desempeño en base a las evaluaciones estandarizadas aplicadas desde la Secretaría de Educación de México. Tras la identificación de las necesidades se ha diseñado una estrategia de trabajo para poner en marcha con el alumnado, la cual se enfoca en el trabajo del pensamiento crítico en la asignatura de matemáticas como un instrumento para la mejora de los resultados. A lo largo del artículo se presentará la propuesta educativa de esta práctica, en qué consiste la estrategia y cómo se ha puesto en marcha. Así mismo se presenta una comparativa entre los resultados obtenidos desde el inicio de la misma, teniendo en cuenta los resultados finales y comparándolos con los obtenidos en el diagnóstico.
Palabras clave: Pensamiento crítico; Estrategia didáctica; Desempeño; Mejora educativa.
Abstract
Given the need to raise performance levels in the area of mathematics and Spanish, Technical High School # 28 takes actions to design a strategy to improve results at the beginning of the 2021-2022 school year and subsequent years; these results had the school identified by its low performance based on standardized assessments applied by the Ministry of Education. After the identification of the needs, a work strategy has been designed to be implemented with the students, which focuses on the work of critical thinking in the subject of mathematics as an instrument for the improvement of results. Throughout the article, the educational proposal of this practice will be presented, what the strategy consists of and how it has been implemented. Likewise, a comparison is presented between the results obtained since the beginning of the practice, taking into account the final results and comparing them with those obtained in the diagnosis.
Keywords: Critical Thinking; Strategy; Performance; Improvement.
Contextualización
Al inicio del ciclo escolar 2021-2022 (agosto 2021) se identificó la necesidad de elaborar una estrategia que permitiera mejorar los niveles de habilidades matemáticas y de lectura de la escuela secundaria técnica número 28 que se ubica en el municipio de El Mezquital en el estado de Durango, en México. La escuela que atiende a una población entre los 11 y los 15 años de edad, se encuentra inmersa dentro de un municipio con una gran cantidad de población indígena, pertenecientes a la etnia Tepehuanos (O´Dam, en su nombre original) y dado a las dificultades propias de la orografía, la economía y la falta de empresas productivas, un alto porcentaje de personas de esta etnia consideran necesaria la migración hacia la cabecera municipal, la cual, al ser la ciudad con más oportunidades de desarrollo, les facilita su progreso personal.
Tras la aplicación de exámenes estandarizados en meses anteriores al inicio del ciclo, refiriéndose este término a las pruebas que aplica la Secretaría de Educación a todas las escuelas para medir el desempeño de las y los alumnos, en las cuales se obtuvo bajo aprovechamiento, el centro educativo fue identificado como una escuela de bajo desempeño, así que fue necesario que todo el colectivo docente implementara acciones que permitieran mejorar los resultados. Estas nuevas estrategias se pusieron en marcha en el ciclo escolar 2021-2022.
Este artículo presenta las acciones que se han realizado desde sus inicios hasta la actualidad, así como la toma de decisiones necesarias para la implementación de esta estrategia. Es importante mencionar que, aunque se realizó únicamente para las dos áreas involucradas (español y matemáticas), este escrito se enfoca en las acciones implementadas en la asignatura de matemáticas. Si bien el examen estandarizado corresponde a las dos asignaturas y aunque en la escuela se implementaron acciones paralelas a estas dos, el artículo habla exclusivamente de una de ellas; cabe mencionar que los resultados obtenidos son muy similares. Se agrega el anexo 1 con un ejemplo de examen estandarizado.
Los resultados que se obtuvieron al finalizar la implementación de dicha estrategia han sido validados por los diferentes instrumentos de evaluación externos que fueron aplicados durante estos ciclos escolares (2021-2022 y posteriores) y son muy significativos con relación a la mejora obtenida. Para la aplicación de dichas estrategias prácticamente se vio envuelto todo el colectivo docente en la toma de decisiones y en un alto porcentaje, casi su totalidad, en la implementación, los cuales colaboran de una manera efectiva para la aplicación de esta metodología.
La etnia tepehuana, para obtener referentes de ella, es una comunidad que, a la llegada de los españoles a la provincia de la Nueva Vizcaya, que actualmente se denomina Durango, al inicio convivió con la llegada de los españoles. En la etapa de conquista, al buscar su independencia de la comunidad española, entran en guerra con los españoles, por lo tanto, son atacados junto con otras tribus regionales aliadas; los españoles buscaron el exterminio total de estas tribus. La comunidad tepehuana es una de las que logran sobrevivir y al ser buscadas para su exterminio huyen hacia lo alto de la zona de la Sierra Madre Occidental, que, como referencia más conocida, son las Barrancas del Cobre de Chihuahua, las cuales se prolongan hasta el sur del Estado de Durango. En ellas habitan actualmente la mayor parte de los tepehuanos, donde por más de 300 años vivieron prácticamente escondidos de la civilización Mestiza y entre sus prácticas y costumbres no tienen contacto prácticamente con las demás comunidades.
Lo anterior, origina que sea una etnia en una zona muy agreste, sin áreas de cultivo y con condiciones muy precarias, tanto de acceso, como económicas y de desarrollo; ante tal motivo se presenta una dificultad muy grande para poder llevar todos los servicios con que actualmente se cuenta en una ciudad, por mencionar, servicios médicos, educación y otros como servicios de telefonía, electrificación y conexión por internet, etc.
La escuela es una institución de educación secundaria de una de las diversas modalidades que se ofrecen en México. Es una escuela de organización completa, que se ubica en la cabecera municipal al inicio de la zona de sierra donde habitan los tepehuanos. La cantidad de alumnos que se manejan ronda los 300 estudiantes por ciclo escolar, divididos en 12 grupos, cuatro grupos por cada uno de los tres grados que se imparten. La comunidad estudiantil está conformada prácticamente por 50% indígena y 50% mestizos.
La escuela se encuentra ubicada en una comunidad de 3500 personas, por lo cual gran parte del alumnado que se tiene corresponde a varias localidades mestizas cercanas, y de alumnos tepehuanos que han decidido viajar de sus lugares de origen, algunos hasta 8 o 10 horas de distancia a pie o a caballo, para llegar a un albergue comunitario, que les ofrece hospedaje para que puedan cumplir con sus estudios; este albergue es compartido con estudiantes de bachillerato y de licenciatura que estudian en la misma ciudad.
El equipo docente con el cual cuenta la escuela, en su gran mayoría, son docentes que viven fuera de esta comunidad, principalmente de la ciudad capital del estado, que se encuentra ubicada a una hora de camino a la cabecera municipal de El Mezquital. Se trata de docentes que han sido asignados a esta escuela por los diferentes métodos de selección que tiene la Secretaría de Educación (nuevo ingreso, cambios de asignación y horas adicionales), de tal forma que es un colectivo escolar con experiencia; cerca del 40% tiene estudios de posgrado en educación. Cabe señalar que ninguno de los docentes pertenece a la comunidad indígena, como sucede en otras escuelas inmersas en la sierra, en este caso, todos son de origen mestizo, los cuales se trasladan para poder desempeñar sus funciones.
Cada año la Secretaría de Educación Pública en el estado, elabora exámenes estandarizados para determinar el nivel de desempeño de cada una de las escuelas, principalmente enfocados en las áreas de matemáticas y de lectura. La intención es determinar cuáles son las habilidades matemáticas y de lectura que manejan cada uno de las y los estudiantes; en estos exámenes estandarizados no se evalúan los objetivos de aprendizaje, sino que más bien se están evaluando las habilidades en cada una de estas áreas mencionadas. En el ciclo escolar 2020-2021, la escuela no obtuvo buenos resultados, por lo cual se señaló como una de las escuelas que requerían más apoyo en este sentido, lo que implicó que durante el ciclo 2021-2022 se tuvieron que implementar algunas acciones para poder revertir dichos resultados.
Justificación Teórica
Para definir el pensamiento crítico podemos decir que es la habilidad de analizar y evaluar información y argumentos para formar un juicio claro y racional. Expertos como Richard Paul y Linda Elder (2003), describen el pensamiento crítico como un proceso intelectual disciplinado. Partiendo de esto y no perdiendo el punto de vista educativo, podemos enfocarnos en que el pensamiento crítico es la parte fundamental de dicho proceso y ahora vamos a explicar por qué.
El pensamiento crítico contribuye significativamente al rendimiento académico de las y los estudiantes. Según Halpern (1998), los estudiantes que son entrenados en habilidades de pensamiento crítico tienden a tener un enfoque más activo hacia su aprendizaje. Esto se traduce en una mayor participación en clase, mejor retención de información y una capacidad superior para aplicar conceptos en diversas situaciones.
Un estudio realizado por Pithers y Soden (2000) resalta que las y los estudiantes que participan en programas que promueven el pensamiento crítico obtienen mejores resultados en pruebas estandarizadas. Esto se debe a que estas habilidades permiten a las y los estudiantes organizar sus pensamientos, formular preguntas relevantes y evaluar la calidad de las fuentes de información. Al estar mejor equipados para abordar problemas complejos, las y los estudiantes pueden mejorar no solo sus calificaciones, sino también su comprensión profunda del material.
Sebastiani Elías (2014) nos dice que el pensamiento es “un proceso activo que involucra una variedad de operaciones mentales importantes como la inducción, deducción, razonamiento, secuencia, clasificación y definición de relaciones” (p. 115). Por esto, el pensamiento crítico no queda fuera de los diferentes planes educativos de diversas naciones.
En la declaración de Incheon, la UNESCO deja de manifiesto en su documento base del Foro Mundial sobre la Educación 2015, el objetivo número 4 relacionado con el ámbito educativo, el cual dice que “garantizará que todas las personas adquieren una sólida base de conocimientos, desarrollen un pensamiento creativo y crítico y habilidades para la colaboración y estimulen su curiosidad, valor y resiliencia” (UNESCO, 2015, p. 15).
En este mismo enfoque la OCDE y el Banco Mundial en sus documentos se alinean también a este objetivo. La Comisión Europea de manera similar también nos dice que: “Toda persona tiene derecho a una educación, una formación y un aprendizaje permanentemente inclusivos y de calidad a fin de mantener, de adquirir capacidades que les permitan participar plenamente en la sociedad” (Comisión Europea, 2019, p. 2).
En México la situación no ha sido diferente, ya que, en los planes de estudio anteriores, desde el año de 1993 ya se hace énfasis en sus propósitos y en los perfiles de egreso. Aunque el plan de estudios lo contempla, no utiliza el término de pensamiento crítico para lograr este punto, pero conociendo la definición, vemos que se está enfocando a la generación del mismo en las y los alumnos.
Si continuamos con el análisis de los planes de estudio, en el Plan de Estudios 2006, en su perfil de egreso en el segundo apartado se maneja como uno de los rasgos importantes: “[…] emplea la argumentación y el razonamiento al analizar situaciones, identifica problemas, fórmula preguntas, emitir juicios y proponer diversas soluciones” (SEP, 2006, p. 10). Si bien, ya se le da un lugar específico al pensamiento crítico dentro del perfil de egreso, no lo maneja de una manera directa como debe ser abordado.
El Plan de Estudios 2011 hace un enfoque mayor en el pensamiento crítico desde la presentación de dicho plan. También hace mención dentro de los principios pedagógicos en su primer principio “centrar la atención en las y los alumnos y sus procesos” (SEP, 2011, p. 22). y “[…] desarrollar habilidades superiores del pensamiento para solucionar problemas, pensar críticamente, comprender y explicar situaciones desde diversas áreas del saber…” (SEP, 2011, p. 22).
De la misma manera, también en el Plan de Estudios 2018 se da énfasis importante en el perfil de egreso, pues se le da todo un ámbito; el cuarto ámbito se llama “pensamiento crítico y resolución de problemas” en el cual se enfocan los cuatro rasgos que deberá cumplir el alumnado en cada uno de sus niveles educativos.
En el Plan de Estudios 2022, la Nueva Escuela Mexicana, desde el perfil de egreso en su rasgo 10 nos está marcando que el pensamiento crítico es una parte sustancial y muy importante que debe tener cada uno de las y los alumnos que egresan de la Educación Básica. También dentro de los ejes articuladores, en particular el cuarto eje, ya maneja lo que viene siendo el pensamiento crítico como una de las partes fundamentales en la formación del alumno (SEP, 2022).
El pensamiento crítico se trata de generar un juicio reflexivo (Facione, 1990) basado en un principio de habilidades en el que interviene la interpretación, el análisis, la evaluación, la inferencia, la explicación y la autorregulación. Supera los últimos niveles de la Taxonomía de Bloom, por lo que la labor del docente realmente da vida y fundamenta en el alumno las bases para poder lograr en él las habilidades de llevar a la práctica el pensamiento crítico.
Matemáticas y pensamiento crítico
Las matemáticas, tradicionalmente consideradas una ciencia exacta, han trascendido los números y fórmulas para convertirse en una herramienta clave en el desarrollo de habilidades cognitivas. En este sentido, el pensamiento crítico —la capacidad de analizar, evaluar y sintetizar información— se ve enriquecido cuando se aborda desde una perspectiva matemática (Franco Alcaraz, 2019). A su vez, fomentar una actitud crítica en el proceso de aprendizaje favorece la resolución de problemas y la comprensión profunda de conceptos matemáticos, como lo demuestran estudios recientes en contextos educativos (Rivera Guerrero et al., 2024). Por lo anterior, se propone un marco teórico integrador en el que matemáticas y pensamiento crítico se potencian de forma bidireccional.
Cómo las matemáticas contribuyen a la formación del pensamiento crítico
El estudio de las matemáticas exige la aplicación de procesos lógicos y secuenciales para deducir teoremas y resolver problemas. Este rigor metodológico obliga a las y los estudiantes a organizar ideas de forma estructurada y a exigir evidencia clara en cada conclusión, fortaleciendo así el pensamiento crítico (Franco Alcaraz, 2019). La sistematización que impone la resolución matemática se traduce en una capacidad analítica que es fundamental para evaluar información en cualquier ámbito.
La práctica matemática implica descomponer problemas complejos en partes más sencillas, identificar variables clave y aplicar estrategias diversas para alcanzar una solución. Estas habilidades no solo son vitales para el éxito académico, sino que también se trasladan a situaciones de la vida real, facilitando la toma de decisiones informadas y el análisis de múltiples alternativas (Rivera Guerrero et al., 2024). El ejercicio constante de este proceso refuerza la agilidad mental y la capacidad de enfrentar desafíos de manera sistemática.
Buscar patrones y relaciones entre elementos es una actividad central en las matemáticas. Esta práctica no solo facilita la memorización, sino que también promueve una comprensión profunda de las estructuras subyacentes en fenómenos complejos. Al aprender a establecer conexiones lógicas, las y los estudiantes desarrollan una visión crítica que les permite prever tendencias y analizar datos de forma objetiva (Bermúdez Mendieta, 2021).
Cómo el pensamiento crítico fortalece las habilidades matemáticas
El pensamiento crítico impulsa a los aprendices a cuestionar supuestos, revisar cada paso en la resolución de problemas y validar resultados. Esta actitud reflexiva es esencial en matemáticas, ya que permite identificar posibles errores y descubrir metodologías alternativas que enriquecen el proceso de aprendizaje (Bermúdez Mendieta, 2021). La revisión constante se convierte, así, en la base para un conocimiento duradero y significativo.
Una mentalidad crítica fomenta la exploración de caminos múltiples a la hora de solucionar problemas matemáticos. Esta flexibilidad permite a las y los estudiantes diseñar estrategias innovadoras y adaptativas, en lugar de seguir un único método preestablecido. La capacidad de generar y evaluar diversas alternativas es una manifestación clara de cómo el pensamiento crítico puede potenciar la creatividad en el ámbito matemático (Rivera Guerrero et al., 2024).
El intercambio de ideas mediante el debate y la discusión colaborativa contribuye a la consolidación de los conceptos matemáticos. Al contrastar diferentes enfoques y argumentar diversas metodologías, se fomenta un ambiente en el que el aprendizaje es dinámico y fundamentado en la evidencia. Esta interacción fortalece tanto la postura crítica como la comprensión profunda de las matemáticas (Franco Alcaraz, 2019).
La relación entre las matemáticas y el pensamiento crítico es inherentemente sinérgica. Mientras que el estudio matemático fortalece habilidades como el razonamiento lógico, la resolución de problemas y la identificación de patrones, el pensamiento crítico impulsa una revisión constante y una actitud flexible en el aprendizaje. Esta interdependencia resulta fundamental para formar individuos capaces de enfrentar desafíos complejos en contextos académicos y profesionales, preparando el terreno para un aprendizaje integral y aplicado (Franco Alcaraz, 2019; Bermúdez Mendieta, 2021; Rivera Guerrero et al., 2024).
Objetivos
En este sentido, el colectivo escolar reflexionó sobre qué estrategia podría ayudar a desarrollar el pensamiento crítico y así mejorar el aprovechamiento académico. Se realizó un diagnóstico censal al inicio del ciclo escolar en el mes de agosto, sobre las habilidades matemáticas y de lectura del total de los alumnos de la escuela. La intención era conocer su desempeño en las evaluaciones estandarizadas. Con los resultados, se desarrolló una reunión por academias en cada una de las asignaturas involucradas, con la intención de conocer cuáles eran las principales debilidades y en plenaria del Consejo Técnico Escolar en el mes de septiembre se tomaron las decisiones correspondientes para su implementación mediante un Plan de Mejora. Se llevó a cabo una evaluación censal de seguimiento a mitad del ciclo escolar en el mes de enero y una evaluación al final del ciclo escolar en el mes de junio, de tal forma que se pudieran medir avances y poder tomar decisiones para el ciclo siguiente.
Es por todo lo anterior que el principal objetivo que se planteó para esta práctica fue:
§ Diseñar una estrategia para el área de matemáticas a desarrollar durante el ciclo escolar 2021-2022 para lograr que las y los alumnos mejoren sus resultados en las próximas evaluaciones estandarizadas.
Que, dentro de esta, a manera de objetivos específicos:
§ Se desarrolle el pensamiento crítico como una herramienta de mejora del rendimiento escolar;
§ también sirva para evitar el rezago en las operaciones básicas, pues ambas cosas se detectaron como una deficiencia en nuestras y nuestros alumnos.
En base a los objetivos anteriores se acordó que para llegar a estos, la estrategia consistiría en la construcción de una serie de fichas con las cuales se pudiera desarrollar el pensamiento crítico como una opción a la mejora del rendimiento escolar, dado que las y los alumnos fueron detectados en los diagnósticos que carecían de algunas de las características distintivas como: analizar un problema, por consecuencia no analizarlo desde diferentes puntos de vista, hacer preguntas para aclarar dudas, jerarquizar argumentos, falta de deducción, no contrastar información o detectar errores e inconsistencias.
Se observó que no podían comprender la intención de un problema, así como identificar el objetivo a realizar en una situación o problema. Aunado a esto se adiciona más información en las fichas para complementarlas, que resultaron del análisis de la situación, como se describe más adelante.
Descripción
En reunión de todo el colectivo docente, al inicio del ciclo escolar y ante los resultados proporcionados por la Secretaría de Educación sobre la aplicación de las pruebas estandarizadas, se tomó como prioridad la mejora de los resultados del aprovechamiento escolar, ante esto y con los resultados de las diferentes pruebas diagnósticas que cada docente realiza a su grupo en la primera semana de clases, se tomó la decisión de reforzar el pensamiento crítico, pues se pudo detectar que no había razonamiento en la resolución de problemas o situaciones planteadas en los diagnósticos. De la misma manera, se decidió determinar los instrumentos de valoración de avances; dichos avances serían medidos al inicio del ciclo escolar, en la parte media y finalmente cerca de concluir el ciclo.
Por la experiencia docente se determinó en la primera reunión que la mayor deficiencia se encontraba en las operaciones básicas, pero no había instrumentos que especificaran en qué áreas de las operaciones básicas se tenía dicha deficiencia, por lo que fue necesario diseñar un instrumento (anexo 2), en el cual, mediante 12 operaciones se pudiera determinar cuál era el nivel de deficiencia que mostraban las y los alumnos, 4 de ellas eran de operaciones con números enteros, 4 con números con decimales, 4 con fracciones y dos problemas.
En la primera semana del ciclo escolar se aplicó dicho instrumento y se evaluó por medio de un concentrado en Excel, el cual demostró mediante números las respuestas resueltas correctamente y la cantidad de aciertos logrados en sentido horizontal, por alumno, y en sentido vertical por reactivo, lo cual nos mostró los números reales que presentaba la escuela.
Se determinó usar los tres niveles de conocimientos y habilidades que manejan las pruebas estandarizadas, que son: Bueno, Suficiente y Requiere Apoyo; donde en “bueno” el estudiante tiene un dominio óptimo de los contenidos, en “suficiente” alcanza los objetivos planteados, y en “requiere apoyo” no alcanza el nivel mínimo esperado.
Al término del cual se obtuvieron los resultados que se muestran en la Tabla 1.
Tabla 1. Resultados de la prueba diagnóstica
|
Nivel de aprovechamiento |
Porcentaje de alumnos en el nivel |
|
Bueno |
29% |
|
Suficiente |
7% |
|
Requiere Apoyo |
64% |
Los resultados que arrojó el desglose por grado y por grupo, así como por alumno y a la vez por reactivo, destacaron que en este punto las operaciones básicas con decimales y con fracciones se encontraron en el punto más alto de deficiencia, ello aunado a que un buen número de las y los alumnos también presentaba deficiencias en la resolución de operaciones con números enteros. Se determinó que en general las operaciones básicas eran un punto a tratar para lograr la mejora.
Al terminar esta fase de diagnóstico y al tener los resultados y el desglose de los mismos, se llevó a cabo una reunión de la academia de matemáticas para analizarlos y determinar las debilidades y las áreas de oportunidad de nuestro alumnado y poder presentar en la siguiente reunión de Consejo Escolar los resultados para que en plenaria se avalaran las decisiones a implementar. Se llevó a cabo la reunión donde se coincidió en los resultados y se generaron posibles soluciones.
En la siguiente reunión de Consejo Escolar se presentaron los resultados y las posibles soluciones, las cuales consistieron en que cada grupo aportaría una clase de la semana para la resolución de ejercicios enfocados en la resolución de problemas que implicaran el razonamiento, el pensamiento crítico enfocado a las matemáticas y las operaciones básicas. Todo esto presentado de manera lúdica a modo de reto para las y los alumnos y que los motivaría a su resolución, ya fuera de manera individual o colaborativa, dependiendo de las necesidades del problema. En los anexos 3 al 5 se agregan algunas fichas de trabajo del total de las aplicadas.
Por acuerdo se determinó que fuera la subdirección quien diseñara el horario de trabajo para que los materiales lúdicos con que se cuenta fueran utilizados eficientemente y evitar los empalmes de grupos para permitir que se tuviera materiales suficientes para elaborar grupos pequeños de trabajo. A su vez, se comisionó a la subdirección y la academia de matemáticas para la elaboración de fichas de trabajo con dichas actividades, bajo la sugerencia de la academia para que toda la escuela pudiera trabajar de manera uniforme y fuera repartido equitativamente el trabajo.
En el Consejo Técnico Escolar se determinó dar seguimiento en la mitad del ciclo escolar, por lo que el mismo instrumento se aplicó de nueva cuenta y se acordó presentar los resultados nuevamente para validar el trabajo o en su defecto realizar cambios.
En la evaluación de seguimiento se determinó que, aunque los datos no fueron muy satisfactorios, sí había avances, por lo que se acordó darle continuidad al trabajo en el mismo sentido que las acciones tomadas posterior a la evaluación diagnóstica y se acordó que se determinarían los avances correspondientes al finalizar el ciclo escolar. Finalmente se realizó la evaluación final para poder conocer los avances logrados. En el anexo 6 se incluye un cronograma con las acciones realizadas.
Criterios y Herramientas de Observación
Cuando el colectivo docente decidió tomar acciones para lograr el objetivo planteado, surgieron una serie de cuestionamientos sobre cómo poder determinar las acciones a realizar.
El primer reto que se presentó fue elaborar un instrumento para conocer nuestra condición inicial; se determinó el construir un examen en el cual se pudiera medir lo más importante, las operaciones básicas y la resolución de problemas. En base a los diagnósticos elaborados por cada docente de matemáticas, conocimos que se presentaban dos retos interesantes: el nivel de desempeño con las cuatro operaciones básicas con enteros, decimales y fracciones y un segundo reto, la falta de estrategias en la resolución de problemas que implican operaciones básicas.
La construcción del instrumento quedó de la siguiente manera (anexo 2):
§ 4 operaciones básicas con números enteros (una suma, una resta, una multiplicación y una división).
§ 4 operaciones con números decimales (misma distribución que la anterior).
§ 4 operaciones con números expresados en fracciones.
§ 2 problemas de aplicación de operaciones que impliquen razonamiento.
Se considera que los problemas tienen mayor peso en su valoración, donde se valora la identificación de los datos, las operaciones a utilizar, los procedimientos de resolución de las operaciones y la expresión de los resultados. Se procuró que el diseño de los problemas no fuera de aplicación directa de una sola operación, sino que intervinieran al menos dos operaciones para la resolución del problema.
Con base a lo anterior, se determinó aplicar el instrumento a los tres grados, dado que se presentaba la misma problemática en los mismos (en México, la educación secundaria se divide en tres grados).
El instrumento se construyó de tal forma que pudiera resolverlo un alumno promedio en menos de una sesión que en nuestro caso es de 50 minutos. En el caso de que algún estudiante presentara dificultades, no podíamos usar más tiempo del establecido.
Ahora bien, al analizar el instrumento lo importante no es enfocarnos en la calificación individual obtenida por alumno, sino ubicarlos en uno de los tres niveles de desempeño: alumnos con habilidades buenas, alumnos con habilidades suficientes y alumnos que requieren apoyo, que equivalen a 100-80% de los reactivos correctos, 79-60% y menos que 60% de los reactivos, respectivamente. Esta fue la medición más importante y la que se utilizó como referencia para poder determinar si el aprovechamiento iba mejorando.
Por otro lado, también se vio necesario determinar qué habilidades tenían las y los alumnos en el uso de las operaciones, pues como se comentó anteriormente, se identificó en el primer diagnóstico que había dificultades en el uso de las operaciones básicas. Por ello se elaboró una tabla (anexo 7), donde se pudiera observar en cada fila los resultados por operación por alumno y determinar su nivel de reactivos correctos. El análisis por columnas nos permitió también determinar el número de respuestas correctas por reactivos; este análisis nos permitió determinar sobre qué operaciones deberíamos de hacer énfasis en las fichas de trabajo. En el anexo 7 se muestra cómo se registran las respuestas del instrumento aplicado para el análisis comentado.
Ya elaborado el instrumento, se determinó la aplicación del mismo en tres momentos, al inicio en el mes de agosto, durante el curso en el mes de enero y al finalizar el curso en el mes de junio, como se comentó anteriormente. Y en base a los resultados del diagnóstico se determinó que se trabajaría con fichas didácticas, una por semana en cada uno de los grupos, con un horario establecido por la subdirección de la escuela, de manera rotatoria para que no siempre fuera en la misma clase y día, permitiendo de esta manera que se alternara entre diferentes asignaturas y diferentes maestros por consecuencia, y no fuera repetido para el mismo maestro y asignatura; para el caso de la estrategia de matemáticas participaron los docentes de las áreas de matemáticas, ciencias y tecnologías.
Se encomendó a la academia de matemáticas la construcción de las fichas, considerando para su diseño abordar dos cosas: el desarrollo del pensamiento crítico y el reforzamiento de las habilidades en la resolución de operaciones básicas. Se diseñaron entonces 30 fichas en las cuales se consideraron estas dos prioridades; algunas solo abordan una de ellas, la gran mayoría abordan las dos, y su aplicación fue de manera general en toda la escuela. En los anexos 3 al 5 se agregan algunas de las fichas.
La academia de matemáticas consideró desarrollar el pensamiento crítico en cada ficha, en donde se procuró que el alumno autoevaluara cada una de sus acciones, que juzgara en comparación con las otras estrategias presentadas por sus pares, que dialogara y llegara a acuerdos con sus compañeras y compañeros para la construcción o mejora de sus propios procesos en la resolución de problemas planteados. Bajo estas consideraciones se planteó, que al mismo tiempo que desarrollaran habilidades matemáticas, también se fomentaría el pensamiento crítico. Si bien, no todas las fichas abarcaron las dos prioridades planteadas, habilidades matemáticas y resolución de problemas, en todas las fichas se procuró desarrollar el pensamiento crítico y la autoevaluación que el alumno realiza de sus acciones.
En la actualidad, la enseñanza se orienta cada vez más hacia metodologías que promueven la autonomía de la y el estudiante. La autoevaluación, definida como el ejercicio en el que los propios alumnos reflexionan sobre su desempeño y progreso, es una herramienta clave en este proceso. Al asumir la responsabilidad de evaluar su aprendizaje, las y los estudiantes desarrollan un nivel superior de autoconciencia y pensamiento crítico, ya que deben analizar objetivamente sus resultados, detectar errores y proponer estrategias de mejora (Educar21, 2024).
La autoevaluación actúa como un mecanismo que facilita la metacognición, ya que invita a las y los estudiantes a reflexionar sobre qué y cómo han aprendido. También impulsa la formación del pensamiento crítico de varias maneras:
§ Desarrollo del análisis reflexivo: al evaluar su propio desempeño, las y los estudiantes se ven obligados a cuestionar sus métodos, validar resultados y reconocer la relevancia de cada paso en el proceso educativo. Esto fortalece la capacidad de analizar argumentos y de tomar decisiones fundamentadas (Educar21, 2024).
§ Estimulación de la curiosidad intelectual: la autoevaluación fomenta una actitud inquisitiva, en la que las y los alumnos no se quedan con respuestas superficiales, sino que buscan comprender el "porqué" de sus resultados y las implicancias de sus errores, lo que es esencial para el pensamiento crítico.
§ Fomento de la autonomía en el aprendizaje: al asumir la responsabilidad de su progreso, las y los estudiantes se empoderan para buscar recursos, plantear hipótesis y validar sus conclusiones de manera independiente, aspecto crucial en el desarrollo de una actitud crítica y analítica (Li, 2024).
Diversas estrategias pueden facilitar la incorporación de la autoevaluación como herramienta para potenciar el pensamiento crítico:
§ Uso de rúbricas claras: establecer criterios de evaluación específicos para cada actividad permite a los estudiantes autoevaluar su desempeño de forma objetiva y transparente.
§ Diarios de reflexión: invitar a los estudiantes a llevar un registro de sus aprendizajes y desafíos facilita el seguimiento de su evolución, promoviendo la identificación de patrones y áreas de mejora.
§ Portafolios de aprendizaje: la recopilación de evidencias y trabajos en un portafolio favorece la revisión periódica del proceso de aprendizaje y el análisis crítico de su progreso.
§ Sesiones de retroalimentación: Combinar la autoevaluación con dinámicas grupales en las que se compare y discuta el desempeño individual fortalece la capacidad de argumentar y de recibir críticas constructivas (Educar21, 2024; Li, 2024).
La autoevaluación emerge como una estrategia pedagógica esencial para el fomento del pensamiento crítico en las y los estudiantes. Al reflexionar de manera sistemática sobre su propio aprendizaje, las y los alumnos no solo adquieren una mejor comprensión de sus competencias, sino que también desarrollan habilidades analíticas y reflexivas clave para la toma de decisiones. Este proceso potencia una actitud crítica que trasciende el ámbito académico y se aplica en la resolución de problemas cotidianos, preparando a los estudiantes para enfrentar con éxito los retos del siglo XXI.
También se acordó que, al finalizar el ciclo, se compararían los resultados obtenidos con nuestro propio instrumento, pero también los resultados obtenidos por las evaluaciones estandarizadas externas, de tal manera que una pudiera reforzar los resultados de la otra evaluación, y determinar si se logró un avance o no en el desarrollo de la estrategia.
Resultados, Retos y Dificultades
Para poder realizar las mediciones de los resultados en las reuniones de docentes se acordó que se realizaría una comparativa de los resultados del inicio del ciclo escolar con los resultados al finalizar el ciclo.
Se determinó en plenaria que los avances logrados son efectivos y aparte son corroborados con las evaluaciones estandarizadas, en las cuales se confirmó que el avance es similar en ambos casos, lo que da certeza a dichos resultados.
Realizando la comparativa tenemos los datos que se expresan en la Tabla 2.
Tabla 2. Resultados finales (instrumento interno)
|
Nivel de aprovechamiento |
Porcentaje de alumnos en el nivel |
||
|
Diagnóstico |
Intermedia |
Final |
|
|
Bueno |
29% |
34% |
38% |
|
Suficiente |
7% |
11% |
18% |
|
Requiere Apoyo |
64% |
55% |
44% |
Como se puede apreciar, se obtuvo un avance significativo en los resultados, realizando la comparativa del examen diagnóstico del inicio del ciclo escolar a la evaluación final obtenida al término del mismo; en el nivel Requiere Apoyo, que es el nivel en el cual las y los alumnos no manifiestan los conocimientos y habilidades mínimas, se logró bajar considerablemente el porcentaje, dado que se presentó un avance de 20 puntos porcentuales. También en el siguiente nivel, que corresponde a los conocimientos suficientes para que un alumno pueda presentar un nivel de conocimiento aceptable, se logró un avance de 11%. Finalmente, en el último nivel se logró un avance de 9%, en términos generales, se presentó un avance significativo en todos los niveles que se analizan, si bien hay alumnos con avance significativo en lo individual, también hay alumnas y alumnos que no manifiestan ningún avance, los cuales son focalizados para el trabajo en lo individual durante el próximo ciclo.
En consecuencia, lograr bajar el porcentaje de alumnos que se encuentran en el nivel más bajo y subir el porcentaje de los niveles de Suficiente y Bueno, es un éxito obtenido pues significa que todo el alumnado mejora sus niveles de desempeño.
Dentro de las limitaciones detectadas, al inicio del trabajo se presentó la resistencia normal al cambio de actividad por parte del colectivo docente, pero al haber consensuado las actividades a realizar, nos permitió vencer dicha resistencia y continuar los esfuerzos, que se ven reflejados desde la evaluación intermedia. Aunque los resultados no fueron significativos, si permitieron que se pudieran observar avances, los cuales motivaron al personal docente a continuar por el mismo camino y esperar los resultados definitivos.
Por parte del alumnado hay que considerar que, al inicio de la aplicación de las fichas de trabajo, la dificultad presentada fue considerable, pues se detectó que las habilidades de pensamiento crítico no estaban tan desarrolladas en la mayoría de estos; esto implicó un mayor esfuerzo al inicio de estas actividades. Con el desarrollo de las mismas poco a poco fueron profundizando en el análisis y en la formación del pensamiento crítico.
Un punto relevante, que vale la pena mencionar, fue el romper con costumbres y tradiciones. La mayoría de las y los jóvenes de la región están acostumbrados a desarrollarse en un patrón en el cual la figura principal de la familia toma la mayoría de las decisiones y el grupo familiar no analiza ni cuestiona las decisiones tomadas por el jefe de la familia, por ello no desarrollan como en otros entornos, su pensamiento crítico. Por su parte, los pertenecientes a los mestizos también presentan algunos de estos rasgos, comparados con otros habitantes del estado.
Cabe hacer mención también, que durante el ciclo escolar la escuela estuvo sujeta a la aplicación de exámenes estandarizados, los cuales también manifiestan avances similares en cuanto al progreso mostrado en esta actividad, lo que da validez a la estrategia. Los resultados coinciden en cada uno de los momentos de evaluación, por lo que el avance no presenta sesgos significativos en cada una de las evaluaciones.
Tabla 3. Resultados finales SisAT (Sistema de Alerta Temprana, evaluación estandarizada externa)
|
Nivel de aprovechamiento |
Porcentaje de alumnos en el nivel |
|
|
Diagnóstico |
Final |
|
|
Bueno |
23% |
33% |
|
Suficiente |
10% |
23% |
|
Requiere Apoyo |
67% |
44% |
Discusión y Conclusiones
Después de realizar las actividades durante el ciclo escolar, se pudo determinar que en efecto, el trabajar en las y los alumnos con el pensamiento crítico les proporciona las herramientas necesarias para que tengan una mayor capacidad de análisis, les brinda las habilidades para la resolución de problemas que afrontan en la vida cotidiana, les permite contar con un amplio bagaje de estrategias y habilidades para la resolución de problemas así como la toma de decisiones fundamentadas, animándolos a reflexionar sobre su propio proceso de aprendizaje y autoevaluar las acciones de las estrategias. Además, les permite no solo memorizar formulas o patrones, sino también entender la lógica que subyace a los conceptos matemáticos. Si bien, no se ha logrado que en todos los niveles educativos se trabaje en este sentido de una manera uniforme, al menos el trabajo en nuestra escuela se está realizando en este sentido para que el alumno sea crítico en la elaboración de estrategias para la resolución de un problema que se le presente.
En el nivel de secundaria, aún es una etapa en la que la y el alumno inicia a confrontar problemas reales y empieza a darles solución con la guía del docente, por lo que trabajar en este sentido brinda las primeras herramientas para la resolución de problemas de una forma crítica, pudiendo analizar el problema, sacar deducciones y proponer estrategias de solución. Es por eso que se determina dar ese énfasis en el desarrollo del pensamiento crítico.
Concluyendo, se puede determinar que al fomentar en las y los alumnos el pensamiento crítico, se presentan mejoras en los aprovechamientos obtenidos en las áreas a trabajar y en las demás áreas del currículo de secundaria. El resultado de esta estrategia se da en las áreas de matemáticas y español, no está exento de que al aplicarse en otras asignaturas se presenten resultados similares.
Se puede concluir que la aplicación de la estrategia diseñada sí da cumplimiento a lo deseado al inicio, pues los resultados pudieron verse con la observación del instrumento diseñado por el colectivo docente, pero además también fue validado con la comparativa realizada con las evaluaciones externas. Cabe aclarar que no se logró un avance deseado, pues no se alcanzó la media de las evaluaciones aplicadas en las todas las escuelas, pero se considera que, si se continúa la aplicación de la estrategia, los resultados van a mejorar.
Es por tal motivo que se determinó que este estilo de trabajo se llevará de manera continua durante los siguientes ciclos escolares. Aunque la escuela ya no ha estado en los últimos lugares y se ha logrado avanzar algunos niveles cercanos a la media nacional, se seguirá insistiendo en la mejora de los resultados a través de la continuación de la estrategia. Hasta el día de hoy se sigue aplicando.
Referencias
Bauman, Z. (2009). Modernidad Liquida. Fondo de Cultura Económica.
Bermúdez Mendieta, J. (2021). El aprendizaje basado en problemas para mejorar el pensamiento crítico. INNOVA Research Journal, 6(2), 77–89. DOI: https://doi.org/10.33890/innova.v6.n2.2021.1681
Comisión Europea (2019). Recomendaciones del consejo de 22 de mayo de 2019. Diario oficial de la Unión Europea. https://eur-lex.europa.eu/legal-content/ES/TXT/PDF/?uri=CELEX:32019H0605(02)&from=ES
Educar21 (2024, 27 de septiembre). Autoevaluación y autoconocimiento: 4 estrategias para el crecimiento académico y la reflexión estudiantil [Con ejemplos]. OpenPlann. https://openplann.com/2024/09/27/autoevaluacion-y-autoconocimiento-4-estrategias-para-el-crecimiento-academico-y-la-reflexion-estudiantil-con-ejemplos/
Facione, P. (1990). Critical thinking: a statement of expert consensus for purposes of educational assessment and instruction. American Philosophical Association.
Franco Alcaraz, A. (2019). Influencia de las matemáticas en el pensamiento crítico. [Trabajo fin de máster, Universidad Internacional de La Rioja]. Reunir. https://reunir.unir.net/bitstream/handle/123456789/8145/FRANCO%20ALCARAZ%2C%20ALEXANDRE.pdf?sequence=1
Halpern, D. F. (1998). Teaching Critical Thinking for Transfer Across Domains: Dispositions, Skills, Structure Training, and Metacognitive Monitoring. American Psychologist, 53(4), 449-455. DOI: https://doi.org/10.1037/0003-066X.53.4.449.
Li, W. (2024, 3 de marzo). Cómo fomentar la autoevaluación y la autorreflexión en los estudiantes. Dynamics And Learning. https://dynamicsandlearning.com/es/post/fomentar-autoevaluacion-autorreflexion-estudiantes/
Paul, R., & Elder, L. (2006). The Miniature Guide to Critical Thinking Concepts and Tools. Foundation for Critical Thinking.
Paul, R., y Elder, L. (2003). Mini-guía para el Pensamiento Crítico. Fundación para el pensamiento crítico. https://www.criticalthinking.org/resources/PDF/SP-ConceptsandTools.pdf
Pithers, R. T., & Soden, R. (2000). Critical Thinking in Education: A Review. Educational Research, 42(3), 237-249. DOI: https://doi.org/10.1080/001318800440579
Rivera Guerrero, B. D., Salazar Pazmiño, L. E., Delgado Olmedo, O. R., y Báez Ponce, S. M. (2024). Desarrollo del pensamiento crítico a través de las matemáticas en educación secundaria. Polo del Conocimiento, 9(9). https://polodelconocimiento.com/ojs/index.php/es/article/view/8027
Sebastiani Elías, Y. F. (2004). Promoviendo el pensamiento crítico y creativo en la escuela. Revista Educación, Cultura y Sociedad, 7, 115-117. http://sisbib.unmsm.edu.pe/bibvirtualdata/publicaciones/umbral/v04_n07/A13.pdf
Secretaría de Educación Pública (1993). Plan y Programas de Estudio 1993 Educación Básica Secundaria. Secretaría de Educación Pública. https://es.slideshare.net/VICMAR871/plan-deestudiossecundaria1993
Secretaría de Educación Pública (2006). Plan y Programas de Estudio 2006 Educación Básica Secundaria. Secretaría de Educación Pública. https://efmexico.files.wordpress.com/2008/04/planestudios2006.pdf
Secretaría de Educación Pública (2011). Plan y Programas de Estudio 2011 Educación Básica Secundaria. Secretaría de Educación Pública. https://www.gob.mx/cms/uploads/attachment/file/20177/Plan_de_Estudios_2011
Secretaría de Educación Pública (13 de agosto de 2018). Aprendizajes Clave para la educación integral. Secretaría de Educación Pública. https://www.gob.mx/sep/articulos/aprendizajes-clave-para-la-educacion-integral
Secretaría de Educación Pública (2022). Plan y Programas de Estudio 2022 Educación Básica Secundaria. Secretaría de Educación Pública.
UNESCO (2015). Educación 2030: Declaración de Incheon y Marco de Acción para la realización del Objetivo de Desarrollo Sostenible 4. UNESCO. https://unesdoc.unesco.org/ark:/48223/pf0000245656_spa
CÓMO CITAR: Soto Huizar, F. (2025). El pensamiento crítico como estrategia de mejora en el área de matemáticas. Revista Pensadero: Conocimiento Docente, vol. 3, p. 84-107. En https://revistapensadero.org/
Anexos
Anexo 1. Capturas de exámenes estandarizados de matemáticas
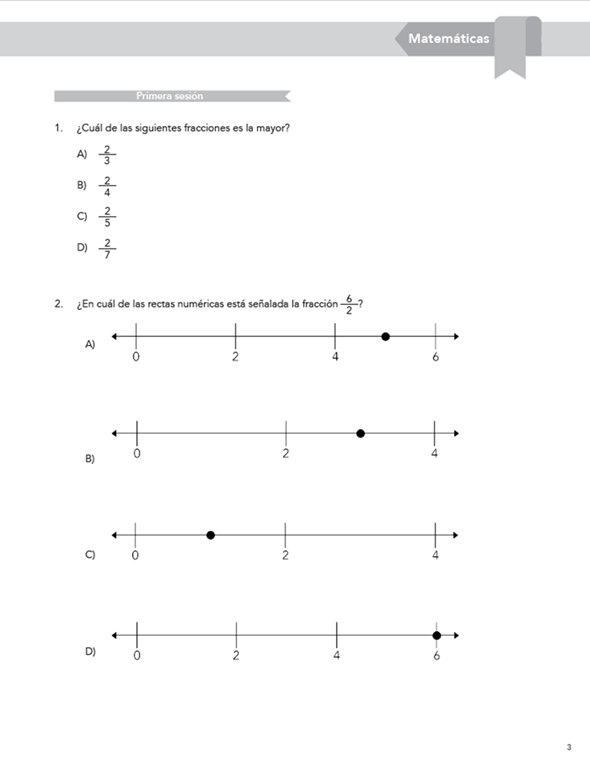


Anexo 2. Instrumento de evaluación
Alumno: ____________________________________________________________
INSTRUCCIONES: Resuelve las siguientes operaciones SIN UTILIZAR CALCULADORA, utiliza los espacios disponibles para realizar tus procedimientos.
a) 128+254+29=
b) 8567-5990=
c) 132 x 45=
d) 128÷46=
a) 2345.84 + 9764.346 + 5467 =
b) 97648.347 – 697.46 =
c) 87.45 x 6.65 =
d) 5979.6 ÷ 13.2 =
Utiliza el procedimiento que consideres adecuado para resolver las siguientes operaciones.
a) ⅔ + ⅕ =
b) ⅖ - ⅛ =
c) ¼ x ⅖ =
d) ⅖ + ¼ =
Problema: ¿Cuántos árboles deberán sembrar en un terreno cercado de 30 x 60 mts si cada árbol para crecer necesita estar separado 5 mts de otros árboles?
Problema: Para hacer un moño de listón se necesitan 45 cm de material. Cada metro tiene un precio de $1.25. ¿Cuánto costará hacer 12 moños?
Anexo 3. Ficha de trabajo 1
Objetivo: Desarrollo del cálculo mental.
Tiempo: 1 sesión (50 min).
Material: libreta de trabajo.
Desarrollo:
El docente enuncia una lista de útiles escolares que se necesitan al inicio del ciclo escolar, se les mencionará que no deben de anotar nada hasta que se les indique, que realizará un cálculo mental de lo que se les solicite.
Problema:
Una mamá va con sus hijos a realizar una compra de útiles escolares para el inicio del ciclo escolar para sus hijos, lleva las dos listas de útiles, una para cada grado que cursan sus hijos, las listas son las siguientes:
Primer grado: Tercer grado
1 Lápiz $4.00 2 Lápices $8.00
1 Pluma $5.00 2 Plumas $10.00
Plastilina $12.50 2 Libretas $35.00
Colores $17.50 Corrector $12.50
Tijeras $14.00 Borrador $3.50
Hojas $17.50 Colores $14.50
La tienda tiene un descuento de 10% si se compra el total de la lista en la tienda.
Se plantea ahora a las y los alumnos una serie de preguntas que contestarán en base a la lista otorgada; si considera necesario puede repetir la lista pero las y los alumnos solo realizan el cálculo mental, de momento no escribirán nada.
¿Cuánto gastaron en total?
¿Cuál lista salió más cara de comprar?
¿Cuánto será el descuento?
Compartan ahora qué estrategias utilizaron para calcular mentalmente cada cantidad.
Finalmente, si el tiempo lo permite, comparen con el cálculo exacto sus estrategias empleadas.